Encryption
Introduction
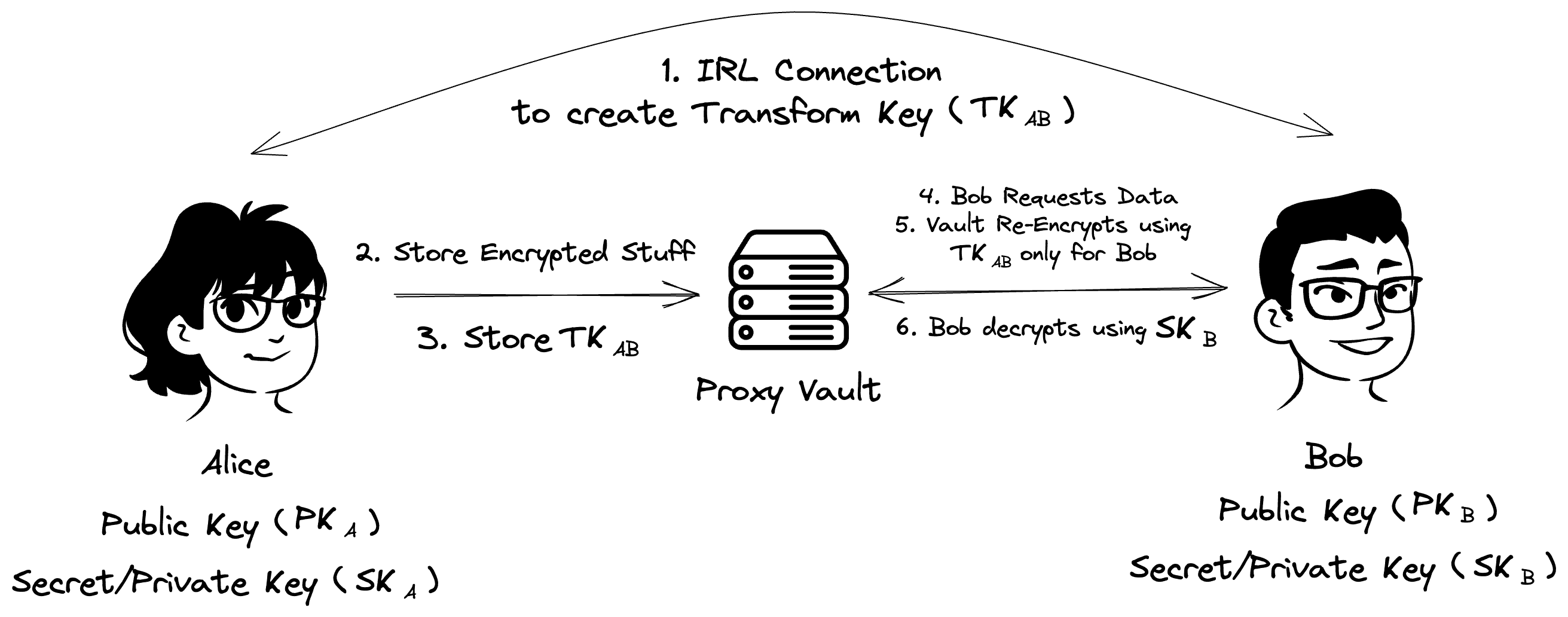
Multi-hop Proxy Re-encryption, also known as Transform Encryption, is a cryptographic technique that allows data encrypted with my public key, to be transformed in a way, so that it can be decrypted using your private key, without revealing either of our private keys. This transformation relies on a special key calculated from my private key and your public key.
More Reading
- https://github.com/ironcorelabs/recrypt-rs
- https://blog.nucypher.com/unveiling-umbral
- https://github.com/yjjnls/recrypt-js
@omnid/pre
A proxy re-encryption implementation using the secp256k1 curve.
Installation
Post-Quantum Security
This is very important in terms of security. https://nvlpubs.nist.gov/nistpubs/ir/2024/NIST.IR.8547.ipd.pdf
Imagine a lattice as a grid of dots, like a pattern of dots on graph paper. This grid is made up of points that are arranged in a repeating pattern. Now, this might seem pretty basic, but these simple grids are the foundation for solving really tough math problems aka NP Hard Problems.
Why do we care about these grids? Well, in the world of cryptography, there's a big concern about the future. You see, someday, powerful quantum computers will break many of the encryption methods we currently use. That would be a problem because it could make our online communication less secure.
So, post-quantum cryptography is all about finding new ways to protect our data from quantum computer attacks. And one of the most promising approaches involves these lattice-based grids.
Let's dive a bit deeper. A lattice is generated by two vectors (or arrows) that start from a central point (the origin). You can think of these vectors like directions or instructions. By stacking these vectors together, we can create paths that reach different points on the lattice. The lattice is basically all the points we can reach by following these "vector paths."
Now, here's the cool part: you can have different sets of vectors that generate the same lattice. Even though the instructions might look very different, they lead to the same destination. It's like having two different ways to get to the same place on a map.
One challenging problem related to these lattices is called the "shortest vector problem." It's all about finding the lattice point that's closest to the origin (0,0) without including the point at the origin itself. This problem is quite tricky, especially as you increase the number of dimensions in the lattice.
Speaking of dimensions, you can have lattices in more than just two dimensions. For example, you can have three-dimensional lattices, four-dimensional ones, and so on. As you add dimensions, the math becomes even more complicated.
Now, these lattice problems, including the shortest vector problem, are considered hard for regular computers to solve. And the good news is that they're also believed to be hard for quantum computers. That's why they're attractive for post-quantum cryptography.
One cryptographic idea involving lattices is called the GGH encryption scheme. In this scheme, you have a "good basis" and a "bad basis" for the same lattice. The good basis is kept secret, while the bad basis is public. When you want to send a secret message, you use the good basis to encrypt it, making it easy for the intended recipient to decrypt. But for someone trying to eavesdrop, only knowing the bad basis makes it incredibly difficult to crack the encryption.
However, GGH encryption has some flaws, so researchers are exploring other lattice-based cryptographic schemes. Some of these schemes use a problem called "learning with errors" to provide strong security against both classical and quantum attacks.
National Institute of Standards and Technology (NIST) has finalised CRYSTALS-Kyber, whose security is based on the hardness of solving the learning-with-errors (LWE) problem over lattices.
In Kyber, there are two main parts: one for creating keys and one for actually encrypting and decrypting messages. These keys are generated by both parties who want to communicate securely in a world with strong quantum computers.